Finite Element Modelling of Moving Loads on Structures

Author: Gareth Forbes Created: 8/8/08 Contact:		Downloads: [D1] Analytical method (matlab) [D2] FEA method (matlab) [D3] FEA method (ANSYS)

Introduction/Background

The problem of moving loads on structures was first considered in the early 19th century when the traversing of bridges by locomotives was analysed, this has been followed by a considerable amount of research on this topic continuing to this day. This problem of a locomotive travelling over a bridge can be solved with various assumptions such as, i) the bridge has negligible mass compared to the moving locomotive, ii) the moving locomotive’s mass is negligible compared to the bridge, or finally iii) the entire system can be dynamically analysed in full when considering the effects of the masses of both the bridge and locomotive.

Fryba’s monograph [1], deals with all of these problems along with numerous others, and is the greatest single point of reference for moving loads on structures. The second type of loading ii), of a point force moving across a single span bridge, was first solved at the beginning of the 20th century by Krylov and continued to include many different types of loading by Timoshenko, cf. [1]. Despite the analytical solution for moving loads on a structure being completed for many different load types a substantial amount of time ago, being able to implement a solution for this type of loading within commercial Finite Element packages is still not a straight forward task. Outlined here will be a method of implementing a moving load, one which is both variable in time and space, in both a commercial Finite Element package, ANSYS (with accompanying script), as well as a simple Finite Element code for solution written for Matlab.This tutorial is not meant to be an exhaustive overview of how to model moving loads with finite element packages, but is aimed at providing enough information and example code to provide a good introduction to someone unfamiliar of this category of modelling.

Analytical formulations The first critical speed of a force travelling across a simply supported beam is shown to occur when the load traverses the length of the beam in the time it takes the first natural frequency to oscillate through one quater of its period. This can be seen in figure (1). Therefore the 1st critical speed of a moving load can be shown to be:   (1) Where ‘n’ is the mode number, ‘l’ is the length of the beam and is the nth mode natural frequency in rad/s.   (2) It can be easily shown that the non-dimensional speed parameter of the ratio of load speed to critical speed can be shown to be   (3) It is also common to have a non-dimensional term for damping which is denoted as:   (4) Where is the logarithmic decrement of damping of the beam. The circular angular frequency of the loads velocity, i.e. converting the horizontal load velocity into a angular velocity of rad/s   (5)

Figure 1. image i) moving force over a single span bridge, when the force velocity = first critical velocity, image ii) midspan beam deflection Figure 2. image i) moving force over a single span bridge, when the force velocity = half first critical velocity, image ii) midspan beam deflection

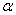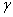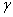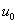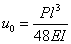
Derivation of the equation for motion for any point and moment in time can be shown to be, with the assumption of only light damping which is practical in most situations [1]: use beta=0.1   (6) If = , and = 1,2,3… Where is the deflection of the beam at mid-span,   (7) If the maximum mid-span deflection of the beam is observed in figures (1)-(3). A curious result is observed as the maximum deflection of the mid-span of the beam occurs at just below the first critical velocity, however at speeds much greater than the lowest critical speed the deflection at the mid-span of the beam is much lower than the static deflection, and maximum dynamic beam deflection. All three figures were produced using the matlab script available with download [D1].

Use of finite elements for solution

Any method of modelling a moving load with finite elements, will require a transient solution method to be used, as a moving load is always transient in nature, ie. no steady state dynamic motion occurs. Use of commercial finite element packages in general do not lend themselves easily towards modelling of such load cases. There exits however dedicated software applications for Finite element analysis of bridge structures under the influence of moving loads, such as BEDAS [2] or ANSYS CivilFEM. BEDAS is a mesh-free or exact stiffness finite element solver which is capable of providing solutions for 2D structures, it provides an GUI for specifying load speeds, magnitude and path. It does not however solve for the dynamics of the body traversing the structure, eg. a vehicle passing over a bridge would be represented by a constant force, and the dynamics of the vehicle are not taken into account. Other in house codes have been developed by researchers for various dynamic loadings and to use with commercial packages, such as the DATIS GUI developed in [3]. Creation of a similar application script should however be easily achieved with the implementation of techniques outlined here.

Figure 4. Simply supported beam with moving load ‘F’ at speed ‘V’

If a simply supported beam is considered, with a moving point load, as shown in figure (4).Then the force for each node will change over time, such that a matrix of all the nodes of interest over the time span wanted, in this case for the time the load is moving across the simply supported beam, can be constructed similar to what is shown in figure (5). (note the force vector does not jump in value from node to node as shown, see [4] for more details). This is essentially what the matlab script available in download [D2] does, with an explicit direct transient solution then employed for the loads on the beam for the respective time step. The method used in download [D3], which provides a routine which can be used directly with the commercial finite element package ANSYS, differs slightly in that the load matrix is not pre-calculated, but the load on each node is calculated for each time step as program solves for the respective load step.

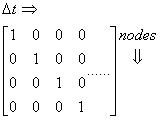
Figure 5. Force matrix of nodes of interest for each time step

The two files, [D2] and [D3], provide examples of how it is possible to model a moving load across a structure and some of the modelling subtleties which need to be considered. The results for the deflection of a single span beam, at load speed of half the first critical speed, using the finite element method in [D2] is shown in figure (6) and can be compared to that which is obtained analytically in figure (2). however it may often be more advantageous to seek a less computationally expensive modal transient solution or perhaps even an implicit solution method.

[1]    Fryba, L., Vibration of solids and structures under moving loads. 3rd ed. 1999, London: Thomas Telford. xxvii,494 p.
[2]     http://www.mechatools.com/BDS/bedas.htm
[3]     Liu, K., G. De Roeck, and E. Reynders. Experimental validation of the dynamic analysis of high speed composite railway bridge. in EURODYN 2008. 2008. Southampton, UK.
[4]     Wu, J.-J., A.R. Whittaker, and M.P. Cartmell, Use of finite element techniques for calculating the dynamic response of structures to moving loads. Computers and Structures, 2000. 78(6): p. 789-799.